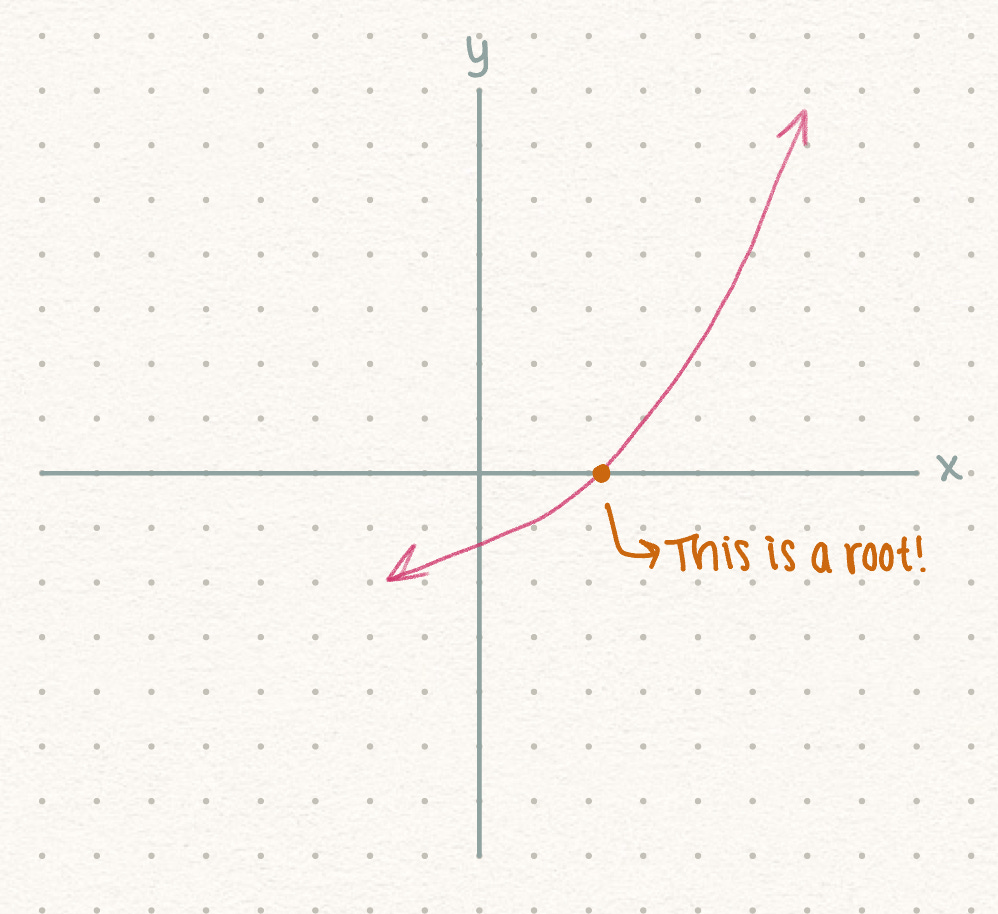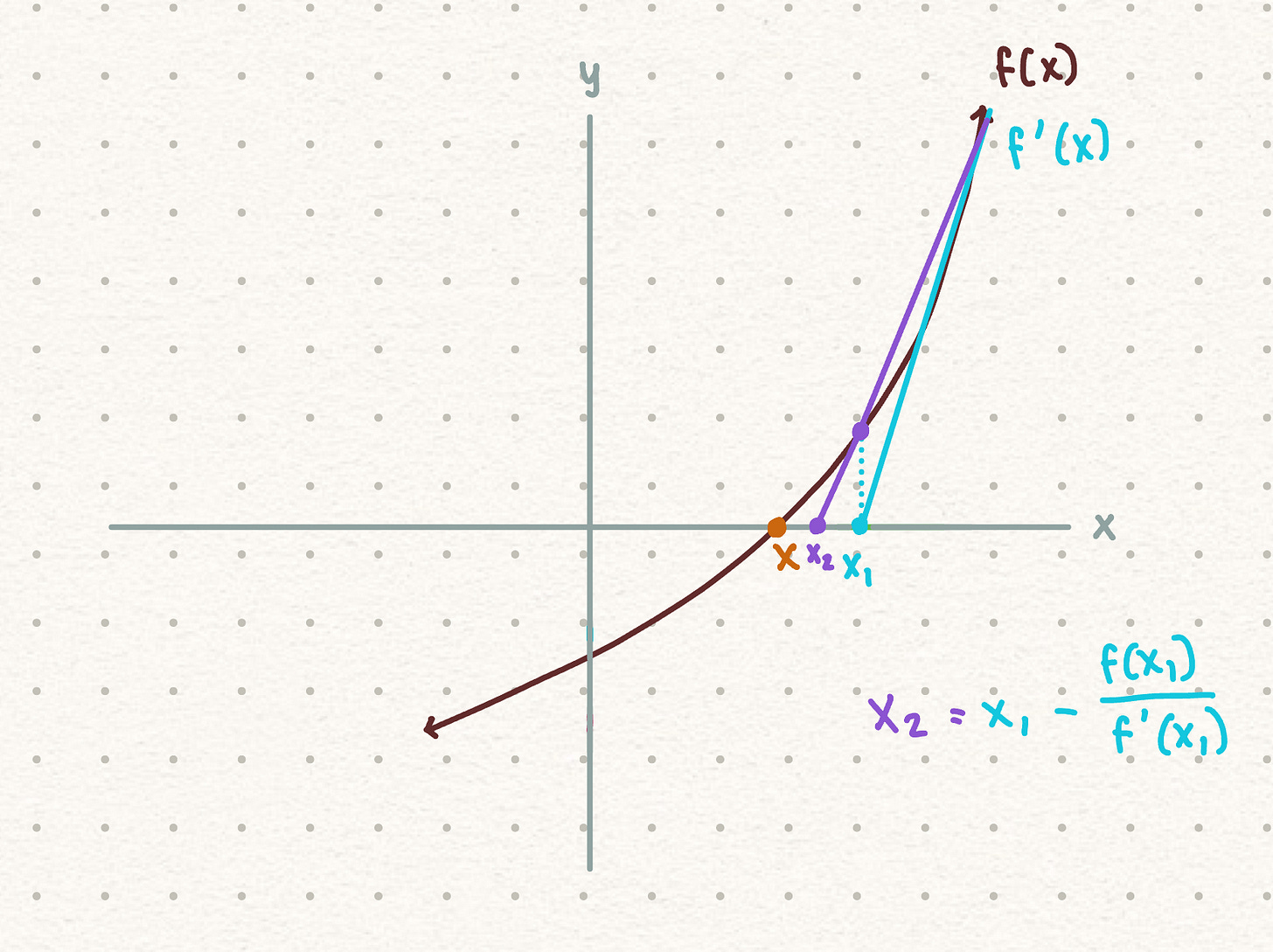Newton-Raphson Method

Approximating Functions Part 2

Hello, friends! Last time, we delved into Taylor Polynomials, which helped us simplify complex functions into to easier to deal with polynomials.

In today's post, we'll explore the Newton method, which is particularly useful for finding approximations for the roots of nonlinear functions.

Roadmap:

1. Newton method

   1. What is Newton method?

   2. What kind of function is this best for approximating?

   3. How does the Newton method work?

   4. Some practice for understanding the math

   5. Python and Newton application

Newton Beyond the Fallen Apple

As crazy as it sounds, Isaac Newton wasn’t the only one to make groundbreaking discoveries. While he independently discovered gravity, Joseph Raphson played an essential role in establishing what is now known as the Newton-Raphson method for approximating the roots of a function. Despite Raphson's significant contribution, Newton's fame has led to the common name ‘Newton method’.

Before we dive into approximating the root of a function, we must first understand what a root is.

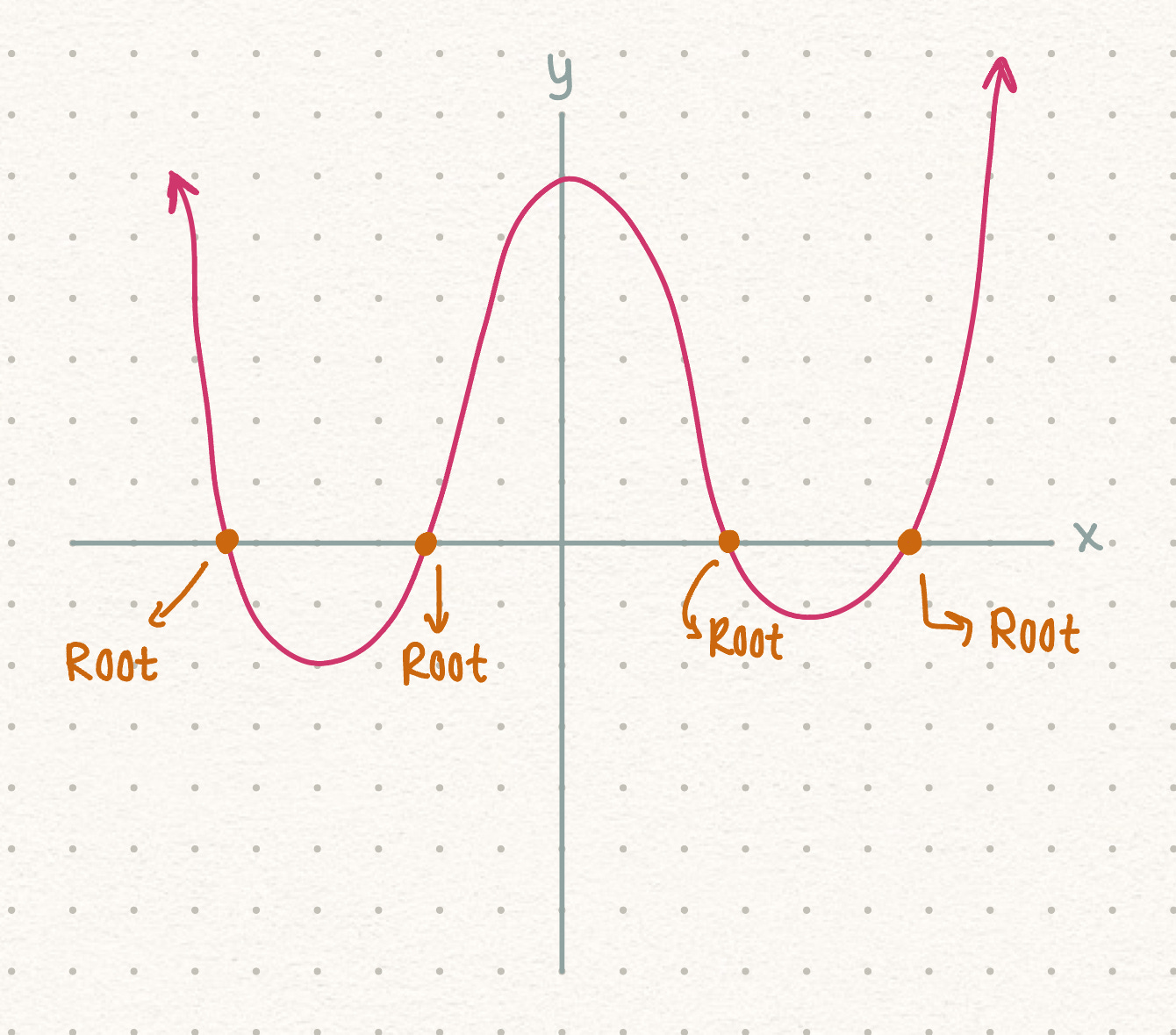
Some functions can have no roots, one root, or many roots! A root, also known as a zero or a solution, occurs when the graph of a function intersects the x-axis.

On a graph, a single root looks like :

Multiple roots can look something like :

Mathematically a root is represented as :

\(\begin{align*} y = 0 \\ f(x) = 0 \end{align*}\)

What Kind of Function is Newton Method best for?

The Newton method uses the concept that a straight tangent line can be used to approximate the roots of a function that is a differentiable and continuous.

Newton method uses iterations to refine its guesses for the root it’s seeking to estimate by using its derivative. With each iteration, it approximates the behavior of the function near our initial guess for the root by using the tangent line at that point. Because of this, a differentiable function (or at least differentiable around the root) works best with the Newton method. If it’s not differentiable, then the tangent line concept fails, and the method may not converge to the root that we’re aiming to approximate.

A continuous function is one that doesn't have breaks, which makes it smooth and reliable.

A function that is discontinuous and non-differentiable can have erratic behavior that can make convergence difficult so using a function that is continuous and differentiable works best with Newton’s method.

Since we now understand what kind of functions work best with the Newton method, let’s look at how the Newton method works to approximate the roots of functions.

How does the Newton Method Work?

Here is a great video that goes into the derivation of the Newton method which I will be expanding on below¹.

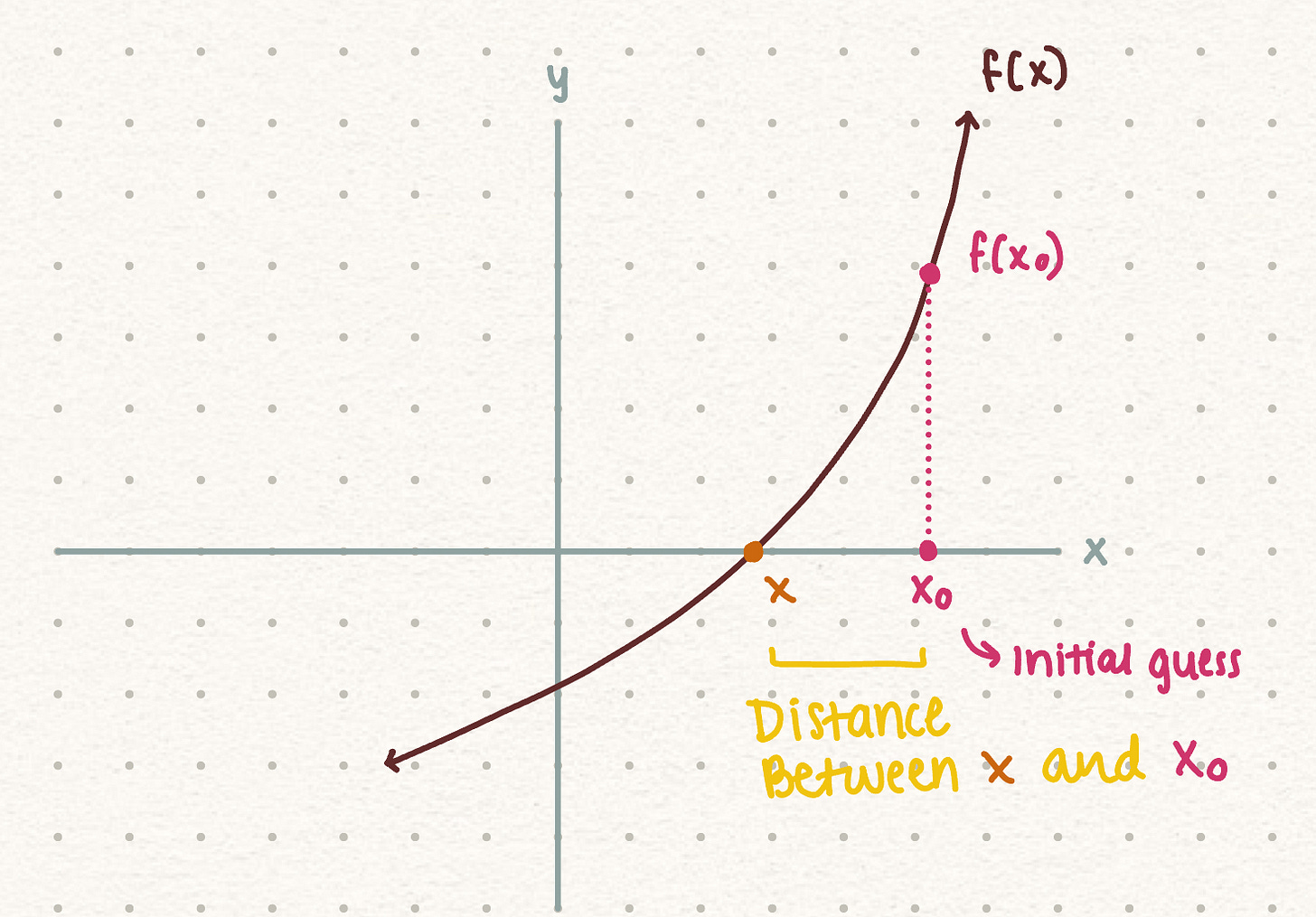
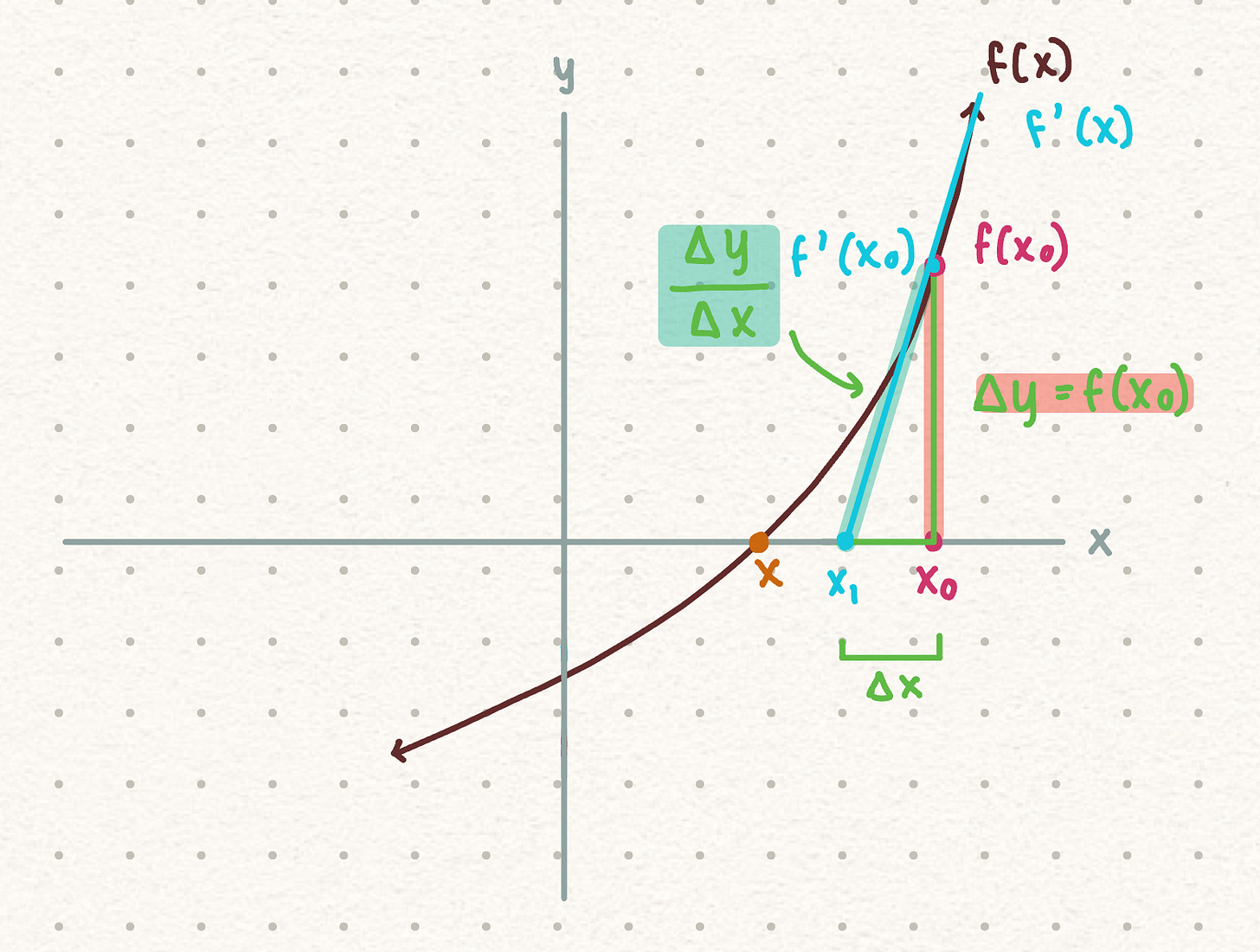
Suppose we have a curve that intersects with the x axis and we want to find the root of this function.

Figure 1

The first thing we would do is make an initial guess.

Figure 2

Next, we want to look at the behavior of the original function at x0, and determine the distance between the real root and our initial guess.

Figure 3

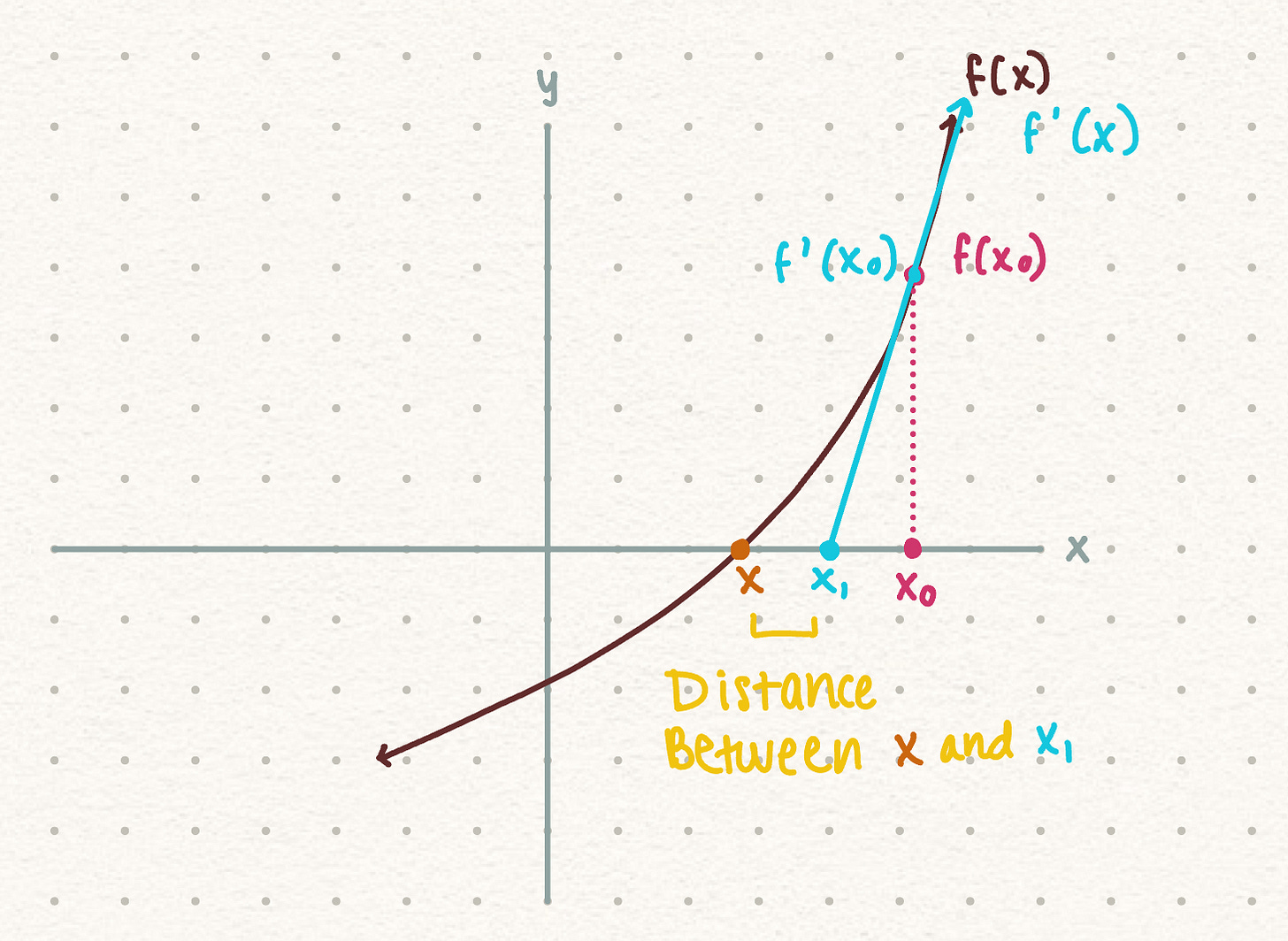
Our initial guess is just a random point that we picked. In order to make our guess better, we will draw a tangent line from f(x0) to get x1.

Figure 4

How much better is x1 compared to our initial guess? In order to find that we devise a expression

\(\begin{align*} x_1 = x_0 - \Delta{x} \end{align*} \)

Figure 5

1. We know the derivative of the original function f(x) is f’(x), which gives us the tangent line:

\(\begin{align*} \frac{d}{dx}f(x) = f'(x) \end{align*}\)

2. Since we used the point f(x0) to draw the tangent line, we want to evaluate when x is equal to x0:

   \(\begin{align*} f'(x)\Bigg|_{x = x_0} = f'(x_0) \end{align*}\)

3. We know that the slope of any function is rise over run, and the derivative of the function gives us the slope of the tangent line. Because of this equality, we can set the following equal to each other:

   \(\begin{align*} f'(x_0) = \frac{\Delta y}{\Delta x} \end{align*}\)

4. We know that the change in y is the same as f(x0) from figure 5:

   \(\begin{align*} f'(x_0) = \frac{\Delta y}{\Delta x} = \frac{f(x_0)}{} \end{align*}\)

5. Now that we have all the known components, we can rearranged this expression as follows to get the change in x:

   \(\begin{align*} \Delta x = \frac{f(x_0)}{f'(x_0)} \end{align*}\)

6. Looking back at figure 4, we found the distance of x1 is equal to x0 minus the change in x.

   \(\begin{align*} x_1 = x_0 - \Delta{x} \end{align*}\)

7. Since we now have a expression for the change in x, we can replace change in x with our expression as follows:

   \(\begin{align*} x_1 = x_0 - \frac{f(x_0)}{f'(x_0)} \end{align*}\)

• x1 = current approximation of the root

• x0 = initial guess for the root

• f(x0​) = value of the function f(x) at the initial guess x0. This gives us the function value at the initial approximation.

• f’(x0) = gives us the slope of the function at x0

• the ratio f(x0) / f’(x0) = represents how far off our initial guess x0 is from the actual root of the function. Dividing the function value by its derivative gives us an estimate of how much we need to adjust x0 to get closer to the root.

In order to improve our approximation, we will now draw another tangent line for x2 from f(x1):

The same process repeats and we get the expression:

\(\begin{align*} x_2 = x_1 - \frac{f(x_1)}{f'(x_1)} \end{align*}\)

This leads us to the Newton method formula:

\(\begin{align*} x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)} \end{align*}\)

• As we increase the number of iterations, we expect the approximation to get closer to the actual root of the function f(x). This means that the difference between the present approximation and previous approximation decrease with each iteration, indicating convergence towards the root.

• A decreasing change in x between iterations signifies that we are refining our approximation and getting closer to the actual root.

• More iterations usually lead to better approximation of the root, especially if the method is converging effectively.

• When the initial guess is far from the root, the convergence may be slower.

There are two main ways we check for convergence.

1. Method 1 :

   \(\begin{align*} |f(x_{n+1})| < \varepsilon \end{align*}\)

   This method states that the absolute value of the function at our updated approximation should be less than the tolerance (ε) in order to state that convergence has been satisfied.

   1. Tolerance is a small positive number (ex. 10 to the negative 8th power) which is how close we want to get to the root. The smaller the value of ε, the more accurate our approximation will be. We will expand tolerance in the coding section.

2. Method 2:

   \(\begin{align*} |x_{n+1} - x_n |< \varepsilon \end{align*}\)

   This method states that converge has occurred when the absolute value of the difference between the updated and previous approximation is less than the tolerance we have set.

Now that we understand what the Newton method is, let’s do some math practice!

Newton Math Practice

Here are a couple great videos to understand the math behind the Newton method²³

Newton and Python

To begin we will create a function called ‘Newton’ for now we will be looking at functions that have a single root:

def Newton(f, df, x0, tol= None, itmax=100, method = None):
    i = 0
    x = x0
    if method == 1: 
        while i < itmax and np.abs(f(x)) > tol:
            x = x - (f(x)/(df(x)))
            i += 1
        print('Method 1')
        return x, i, np.abs(f(x)) 
        
    
    prev_x = x
    if method == 2: 
        while i < itmax and np.abs(x - prev_x) < tol:
            prev_x = x
            x = x - (f(x)/(df(x)))
            i += 1
        print('Method 2')
        return x, i, np.abs(f(x)) 

Breakdown of the code:

1. def Newton(f, df, x0, tol=None, itmax=100, method=None):

   • This line defines the function Newton which takes five parameters:

     • f: the function whose root we are trying to find.

     • df: the derivative of the function f.

     • x0: the initial guess for the root.

     • tol: the tolerance level for convergence. Setting it to be none, so when we apply it to a specific function, we can adjust the tolerance.

     • itmax: the maximum number of iterations.

     • method: the method we will be using to check for convergence.

2. i = 0 and x = x0

   • Initialize the iteration counter i to 0 and the current approximation x to the initial guess x0.

3. if method == 1: and if method == 2:

   • These conditionals check which convergence method is selected.

   • method == 1: Convergence is determined based on the absolute value of f(x) being less than the tolerance tol.

   • method == 2: Convergence is determined based on the absolute difference between the previous approximation prev_x and the current approximation x being less than the tolerance tol.

4. Inside each conditional block, there's a while loop that iterates until one of the convergence conditions is met or the maximum number of iterations (itmax) is reached.

5. The iteration step within the loop is the core of the Newton-Raphson method:

   • x = x - (f(x) / df(x)): This updates the current approximation x using the formula of the Newton-Raphson method.

   • For method 2, it also updates prev_x to keep track of the previous approximation for comparison.

6. After the loop, the function prints a message indicating which method was used and returns a tuple containing the final approximation x, the number of iterations i, and the absolute value of f(x).

Example :

To make sure our function works, lets test it with a function :

\(\begin{align*} f(x) = x^3 - 9 \end{align*} \)

def f(x): 
        return x**3 - 9
    def df(x): 
        return 3*x**2
    x = np.linspace(-10, 10, 100)
    plt.plot(x, f(x)) 
    print(Newton(f, df, 1, tol = 1E-8, itmax=100, method = 1))
    print(Newton(f, df, 1, tol = 1E-8, itmax=100, method = 2))

Output: 

Method 1 - when the absolute value of the function at the current approximation is less than the tolerance. Thus, Convergence has occurred.
(2.0800838232385224, 6, 2.4223503203302243e-09)

• The root approximation: 2.0800838232385224

  • This is quite a good approximation because the real root is 2.08008382305.

• The number of iterations required to reach convergence: 6

• The absolute value of the function at the root approximation: 2.4223503203302243e-09 (a very small number close to zero, indicating convergence)

Method 2 - When the difference between the previous and present approximation is less than the tolerance, Thus, Convergence has occurred.
(3.6666666666666665, 1, 40.29629629629629)

• The root approximation: 3.6666666666666665

• The number of iterations required to reach convergence: 1

• The absolute value of the function at the root approximation: 40.29629629629629

• Method 1 provided a more accurate root approximation (2.0800838232385224) with a small residual value (2.4223503203302243e-09).

• Method 2 provided a less accurate root approximation (3.6666666666666665) with a larger residual value (40.29629629629629).

Here is a video that walks through applying Newton method using Python⁴

Wrap up!

In today’s post we went through a basic overview of Newton method for approximating nonlinear functions, stay tuned for next week’s post on Secant method!

1. Newton-Raphson Formula and Derivation | Part 1 of 2 - Alpha Theta Epsilon (Youtube)

2. Newton Method - The Organic Chemistry Tutor (Youtube)

3. Newton’s method (introduction & examples) - blackpenredpen (Youtube)

4. Newton’s Method In Python | Numerical Methods - StudySession (Youtube)